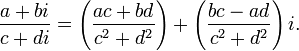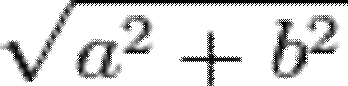Complex number

A complex number can be visually represented as a pair of numbers forming a vector on a diagram called an Argand diagram, representing the complex plane. Reis the real axis, Im is the imaginary axis, andi is the square root of –1.

A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part. In this way the complex numbers contain the ordinary real numbers while extending them in order to solve problems that would be impossible with only real numbers.

Complex numbers are used in many scientific fields, including engineering, electromagnetism, quantum physics, applied mathematics, and chaos theory. Italian mathematician Gerolamo Cardano

is the first known to have conceived complex numbers; he called them "fictitious", during his attempts to find solutions to cubic equations in the 16th century.^[1]

Introduction and definition

Complex numbers have been introduced to allow for solutions of certain equations that have no real solution: the equation

has no real solution x, since the square of x is 0 or positive, so x² + 1 cannot be zero. Complex numbers are a solution to this problem. The idea is to enhance the real numbers by introducing a non-real number i whose square is −1, so that x = i and x = −i are the two solutions to the preceding equation.

Definition

A complex number is an expression of the form

where a and b are real numbers and i is a mathematical symbol which is called the imaginary unit. For example, −3.5 + 2i is a complex number.

The real number a of the complex number z = a + bi is called the real part of z and the real number b is the imaginary part.^[2] They are denoted Re(z) or ℜ(z) and Im(z) or ℑ(z), respectively. For example,

Some authors write a+ib instead of a+bi. In some disciplines (in particular, electrical engineering, where i is a symbol for current), the imaginary unit i is instead written as j, so complex numbers are written as a + bj or a + jb.

A real number a can usually be regarded as a complex number with an imaginary part of zero, that is to say, a + 0i. However the sets are defined differently and have slightly different operations defined, for instance comparison operations are not defined for complex numbers. Complex numbers whose real part is zero, that is to say, those of the form 0 + bi, are called imaginary numbers. It is common to write a for a + 0i and bi for 0 + bi. Moreover, when b is negative, it is common to write a − bi instead of a + (−b)i, for example 3 − 4i instead of 3 + (−4)i.

The set of all complex numbers is denoted by C or .

The complex plane

Figure 1: A complex number plotted as a point (red) and position vector (blue) on an Argand diagram;a + bi is the rectangular expression of the point.

A complex number can be viewed as a point or position vector in a two-dimensional Cartesian coordinate system called the complex plane or Argand diagram (see Pedoe 1988 and Solomentsev 2001), named after Jean-Robert Argand. The numbers are conventionally plotted using the real part as the horizontal component, and imaginary part as vertical (see Figure 1). These two values used to identify a given complex number are therefore called its Cartesian, rectangular, or algebraic form.

The defining characteristic of a position vector is that it has magnitude and direction. These are emphasized in a complex number's polar form and it turns out notably that the operations of addition and multiplication take on a very natural geometric character when complex numbers are viewed as position vectors: addition corresponds to vector addition while multiplication corresponds to multiplying their magnitudes and adding their arguments (i.e. the angles they make with the x axis). Viewed in this way the multiplication of a complex number by i corresponds to rotating a complex number anticlockwise through 90° about the origin.

History in brief

The solution of a general cubic equation in radicals (without trigonometric functions) may require intermediate calculations containing the square roots of negative numbers, even when the final solutions are real numbers, a situation known as casus irreducibilis. This conundrum led Italian mathematician Gerolamo Cardano to conceive of complex numbers in around 1545, though his understanding was rudimentary.

Work on the problem of general polynomials ultimately led to the fundamental theorem of algebra, which shows that with complex numbers, a solution exists to every polynomial equation of degree one or higher. Complex numbers thus form an algebraically closed field, where any polynomial equation has a root.

Many mathematicians contributed to the full development of complex numbers. The rules for addition, subtraction, multiplication, and division of complex numbers were developed by the Italian mathematician Rafael Bombelli.^[3] A more abstract formalism for the complex numbers was further developed by the Irish mathematician William Rowan Hamilton, who extended this abstraction to the theory of quaternions.

Elementary operations

Conjugation

Geometric representation of z and its conjugate in the complex plane

The complex conjugate of the complex number z = x + yi is defined to be x − yi. It is denoted or . Geometrically, is the "reflection" of zabout the real axis. In particular, conjugating twice gives the original complex number: .

The real and imaginary parts of a complex number can be extracted using the conjugate:

Moreover, a complex number is real if and only if it equals its conjugate.

Conjugation distributes over the standard arithmetic operations:

The reciprocal of a nonzero complex number z = x + yi is given by

This formula can be used to compute the multiplicative inverse of a complex number if it is given in rectangular coordinates. Inversive geometry, a branch of geometry studying more general reflections than ones about a line, can also be expressed in terms of complex numbers.

Addition and subtraction

Addition of two complex numbers can be done geometrically by constructing a parallelogram.

Complex numbers are added by adding the real and imaginary parts of the summands. That is to say:

Similarly, subtraction is defined by

Using the visualization of complex numbers in the complex plane, the addition has the following geometric interpretation: the sum of two complex numbers A and B, interpreted as points of the complex plane, is the point X obtained by building a parallelogram three of whose vertices are 0, Aand B. Equivalently, X is the point such that the triangles with vertices 0, A, B, and X, B, A, are congruent.

Multiplication and division

The multiplication of two complex numbers is defined by the following formula:

In particular, the square of the imaginary unit is −1:

The preceding definition of multiplication of general complex numbers is the natural way of extending this fundamental property of the imaginary unit. Indeed, treating i as a variable, the formula follows from this

(distributive law)

(commutative law of addition—the order of the summands can be changed)

(commutative law of multiplication—the order of the factors can be changed)

(fundamental property of the imaginary unit).

The division of two complex numbers is defined in terms of complex multiplication, which is described above, and real division:

Division can be defined in this way because of the following observation:

As shown earlier, c − di is the complex conjugate of the denominator c + di. The real part c and the imaginary part d of the denominator must not both be zero for division to be defined.

Square root

The square roots of a + bi (with b ≠ 0) are 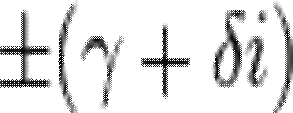, where

and

where sgn is the signum function. This can be seen by squaring to obtain a + bi.^[4][5] Here is called the modulus of a + bi, and the

square root with non-negative real part is called the principal square root.