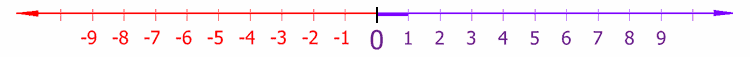Negative number
A negative
number is any real number that is less than zero. Such
numbers are often used to represent the amount of a loss or absence. For
example, a debt that is owed may be thought of
as a negative asset, or a decrease in some
quantity may be thought of as a negative increase. Negative numbers are also
used to describe values on a scale that goes below zero, such as the Celsius and Fahrenheit scales for temperature.
Negative numbers are usually written with a minus sign in
front. For example, −3 represents a negative quantity with a magnitude of
three, and is pronounced “minus three”. Conversely, a number that is greater
than zero is called positive; zero is usually thought of as
neither positive nor negative. The positivity of a number may be emphasized by placing a
plus sign before it, e.g. +3. In
general, the negativity or positivity of a number is referred to as its sign.
In mathematics, every real number other
than zero is either positive or negative. The positive whole numbers are referred
to as natural numbers, while the positive and
negative whole numbers (together with zero) are referred to as integers.
In bookkeeping, amounts owed are often represented by red numbers, or a number in parentheses, as an
alternative notation to represent negative numbers.
Negative numbers appeared for the first time in history in
the Nine Chapters on the Mathematical Art , which in its present form
dates from the period of the Chinese Han Dynasty (202 BC. – AD 220), but may
well contain much older material.[1] Indian mathematicians developed
consistent and correct rules on the use of negative numbers, which later spread
to the Middle East, and then into Europe. Prior to the concept of negative
numbers, negative solutions to problems were considered "false" and
equations requiring negative solutions were described as absurd.[2]
Introduction
As the result of
subtraction
Negative numbers can be thought of as resulting from the subtraction of a larger number from a
smaller. For example, negative three is the result of subtracting three from
zero:
0 − 3 = −3.
In general, the subtraction of a larger number from a smaller
yields a negative result, with the magnitude of the result being the difference
between the two numbers. For example,
5 − 8 = −3
since 8 − 5 = 3.
The number line
The relationship between negative numbers, positive numbers,
and zero is often expressed in the form of a number line:
Numbers appearing farther to the right on this line are
greater, while numbers appearing farther to the left are less. Thus zero
appears in the middle, with the positive numbers to the right and the negative
numbers to the left.
Note that a negative number with greater magnitude is
considered less. For example even though (positive) 8 is greater than (positive) 5, written
8 > 5
negative 8 is
considered to be less than negative 5:
−8 < −5.
In addition, any negative number is less than any positive
number, so
−8 < 5 and −5 < 8.
Signed numbers
In the context of negative numbers, a number that is greater than
zero is referred to as positive. Thus every real number other than zero is either
positive or negative, while zero itself is not
considered to have a sign. Positive numbers are sometimes written with a plus sign in front, e.g. +3 denotes a positive three.
Because zero is neither positive nor negative, the term non-negative is sometimes used to refer to a
number that is either positive or zero, while non-positive is used to refer to a number that is either
negative or zero.
Arithmetic involving negative numbers
The minus sign "−" is used for both the operation of subtraction and to signify that a number is negative. The ambiguity does not generally cause problems in arithmetic, as the result of adding a negative number to another is the same as subtracting the number. A negative number may be parenthesised
with its sign, e.g. an addition is clearer if written 7 + (−5) rather than 7 + −5, and gives the same result as the subtraction 7 − 5.Sometimes in elementary schools a number may be prefixed by a
superscript minus sign or plus sign to explicitly distinguish negative and positive
numbers as in[3]
−2 + −5 gives −7.
Addition
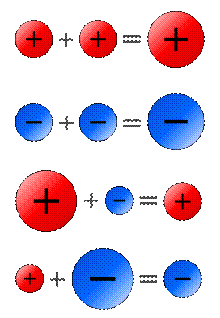
A
visual representation of the addition of positive and negative numbers. Larger balls represent numbers
with greater magnitude.
Addition of two negative numbers is very similar to addition
of two positive numbers. For example,
(−3) + (−5) =
−8.
The idea is that two debts can be combined into a single debt
of greater magnitude.
When adding together a mixture of positive of negative
numbers, one can think of the negative numbers as positive quantities as being
subtracted. For example:
8 + (−3) = 8 − 3 = 5 and (−2) + 7
= 7 − 2 = 5.
In the first example, a credit of 8 is combined with a debt of 3, which yields a total credit
of 5. If the negative number has
greater magnitude, then the result is negative:
(−8) + 3 = 3 − 8 =
−5 and 2 + (−7)
= 2 − 7 = −5.
Here the credit is less than the debt, so the net result is a
debt.
Subtraction
As discussed above, it is possible for the subtraction of two
non-negative numbers to yield a negative answer:
5 − 8 = −3
In general, subtraction of a positive number is the same
thing as addition of a negative. Thus
5 − 8 = 5 +
(−8) = −3
and
(−3) − 5 =
(−3) + (−5) = −8
On the other hand, subtracting a negative number is the same
as adding a positive. (The idea is that losing a debt is the same thing as gaining a credit.) Thus
3 − (−5) = 3 +
5 = 8
and
(−5) − (−8) =
(−5) + 8 = 3.
Multiplication
When multiplying numbers, the magnitude of the product is
always just the product of the two magnitudes. The sign of the
product is determined by the following rules:
The product of one positive number and one negative number is negative.
The product of two negative numbers is positive.
Thus
(−2) × 3 = −6
and
(−2) × (−3) = 6.
The reason behind the first example is simple: adding three −2's together yields −6:
(−2) × 3 = (−2)
+ (−2) + (−2) = -6.
The reasoning behind the second example is more complicated.
The idea again is that losing a debt is the same thing as gaining a credit. In
this case, losing two debts of three each is the same as gaining a credit of
six:
(−2 debts ) × (−3 each) = +6 credit.
The convention that a product of two negative numbers is
positive is also necessary for multiplication to follow the distributive law. In this case, we know that
(−2) × (−3) + 2 × (−3)
= (−2 + 2) × (−3) = 0 × (−3)
= 0.
Since 2 × (−3) = −6, the product (−2) × (−3) must equal 6.
These rules lead to another (equivalent) rule—the sign of any
product a × b depends on the sign of a as follows:
if a is positive, then the sign of a × b is the same as the sign of b, and
if a is negative, then the sign of a × b is the opposite of the sign of b.
Division
The sign rules for division are the
same as for multiplication. For example,
8 ÷ (−2) = −4,
(−8) ÷ 2 = −4,
and
(−8) ÷ (−2) = 4.
If dividend and divisor have the same sign, the result is
always positive.