Commutative
property
Commutativity


4 + 2 =
2 + 4 with blocks
Addition is commutative, meaning that one can reverse the terms in a sum
left-to-right, and the result will be the same as the last one. Symbolically, ifa and b are any two numbers, then
a + b = b + a.
The fact that addition is commutative is known as the
"commutative law of addition". This phrase suggests that there are
other commutative laws: for example, there is a commutative law of
multiplication. However, many binary operations are not commutative, such as
subtraction and division, so it is misleading to speak of an unqualified
"commutative law".
http://www.khanacademy.org/video/commutative-property-for-addition?playlist=Developmental%20Math
Associative
property
Associativity


2+(1+3)
= (2+1)+3 with segmented rods
A somewhat subtler property of addition is associativity
, which comes up when one
tries to define repeated addition. Should the expression
"a + b + c"
be defined to mean (a + b) + c or a + (b + c)? That addition is associative tells us that the
choice of definition is irrelevant. For any three numbers a, b, and c, it is true that
(a + b) + c = a + (b + c).
For example, (1 + 2) + 3 = 3 + 3 = 6 = 1 + 5 = 1 + (2
+ 3). Not all operations are associative, so in expressions with other
operations like subtraction, it is important to specify the order of operations.
Zero and one
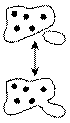

5 + 0 = 5 with
bags of dots
When adding zero to any number, the quantity does not change; zero is the identity element for addition, also known as theadditive identity.
In symbols, for any a,
a + 0 = 0 + a = a.
This law was first identified in Brahmagupta's Brahmasphutasiddhanta in 628, although he wrote it as three separate laws, depending on whether a is negative, positive, or zero
itself, and he used words rather than algebraic symbols. Later Indian mathematicians refined the concept; around the year 830, Mahavira wrote, "zero becomes the same as what is added to it",
corresponding to the unary statement 0 + a = a. In the 12th century, Bhaskara wrote, "In the addition of cipher, or subtraction of it, the
quantity, positive or negative, remains the same", corresponding to the
unary statement a + 0 = a.[10]
In the context of
integers, addition of one also plays a special role: for any integer a, the integer (a + 1) is the least integer greater than a, also known as
the successor of a. Because of this
succession, the value of some a + b can also be seen
as the bth successor of a, making addition
iterated succession.
Units
To numerically add physical quantities with units, they must first
be expressed with common units. For example, if a measure of 5 feet is
extended by 2 inches, the sum is 62 inches, since 60 inches is
synonymous with 5 feet. On the other hand, it is usually meaningless to
try to add 3 meters and 4 square meters, since those units are incomparable;
this sort of consideration is fundamental in dimensional analysis.
http://www.khanacademy.org/video/associative-property-for-multiplication?playlist=Developmental%20Math
In mathematics, and in
particular in abstract
algebra, distributivity is
a property of binary
operations that generalizes
the distributive law from elementary
algebra. For example:
2 × (1 + 3) = (2 × 1) + (2 × 3).
4(8+2) = (4×8) + (4×2) because
4(8 + 2) = 4(10) = 40
(4×8) + (4×2) = 32 + 8 = 40
In the left-hand side of the above equation, the 2
multiplies the sum of 1 and 3; on the right-hand side, it multiplies the 1 and
the 3 individually, with the results added afterwards. Because these give the
same final answer (8), we say that multiplication by 2 distributes over addition of 1 and 3. Since we
could have put any real
numbers in place of 2, 1,
and 3 above, and still have obtained a true equation, we say that multiplication of real numbers distributes over addition of real numbers.
Given a set S and two binary
operations · and + on S, we say that the operation ·
§ is left-distributive over + if, given
any elements x, y, and z of S,
x ·
(y + z) = (x · y) + (x · z);
§
is right-distributive over + if, given
any elements x, y, and z of S:
(y + z)
· x = (y · x)
+ (z · x);
§
is distributive over + if it is both left- and right-distributive.[1]
Notice that when ·
is commutative, then the three
above conditions are logically
equivalent.
1.
Multiplication of numbers is distributive over addition of numbers, for a broad
class of different kinds of numbers ranging from natural
numbers to complex
numbers and cardinal
numbers.
2.
Multiplication of ordinal
numbers, in contrast, is only left-distributive, not
right-distributive.
3.
The cross
product is left- and
right-distributive over vector
addition, though not commutative.
4. Matrix multiplication is distributive over matrix addition, though also not
commutative.
5.
The union of sets is distributive over intersection, and intersection
is distributive over union. Also, intersection is distributive over thesymmetric
difference.
6. Logical disjunction ("or") is
distributive over logical conjunction ("and"),
and conjunction is distributive over disjunction. Also, conjunction is
distributive over exclusive disjunction ("xor").
7.
For real
numbers (or for any totally
ordered set), the maximum operation is distributive over the
minimum operation, and vice versa: max(a,min(b,c)) = min(max(a,b),max(a,c)) and min(a,max(b,c)) = max(min(a,b),min(a,c)).
8.
For integers, the greatest
common divisor is distributive
over the least
common multiple, and vice versa: gcd(a,lcm(b,c))
= lcm(gcd(a,b),gcd(a,c)) and lcm(a,gcd(b,c))
= gcd(lcm(a,b),LCM(a,c)).
9.
For real numbers, addition distributes over the maximum
operation, and also over the minimum operation: a + max(b,c) = max(a+b,a+c)
and a + min(b,c)
= min(a+b,a+c).
In practice, the distributive property of multiplication
(and division) over addition is lost around the limits of arithmetic
precision. For example, the identity ⅓+⅓+⅓ =
(1+1+1)/3 appears to fail if conducted in decimal
arithmetic; however many significant
digits are used, the
calculation will take the form 0.33333+0.33333+0.33333 = 0.99999 ≠ 1.
Even where fractional numbers are representable
exactly, errors will be introduced if rounding too far; for example, buying two
books each priced at £14.99 before a tax of 17.5% in two separate transactions will actually
save £0.01 over buying them together: £14.99×1.175 = £17.61 to the nearest
£0.01, giving a total expenditure of £35.22, but £29.98×1.175 = £35.23. Methods
such as banker's
rounding may help in some
cases, as may increasing the precision used, but ultimately some calculation
errors are inevitable.
http://www.khanacademy.org/video/distributive-property?playlist=Developmental%20Math
1


