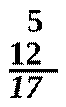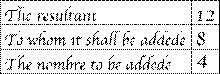Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign (+). For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples. Therefore, 3 + 2 = 5. Besides counting fruits, addition can also represent combining other physical and abstract quantities using different kinds of numbers: negative numbers,fractions
, irrational numbers, vectors, decimals and more.
3 + 2 = 5 with apples, a popular choice in textbooks[1]
Addition follows several important patterns. It is commutative, meaning that order does not matter, and it is associative, meaning that when one adds more than two numbers, order in which addition is performed does not matter (see Summation). Repeated addition of 1 is the same as counting; addition of 0 does not change a number. Addition also obeys predictable rules concerning related operations such as subtraction and multiplication. All of these rules can beproven
, starting with the addition of natural numbers and generalizing up through the real numbers and beyond. General binary operations that continue these patterns are studied in abstract algebra.Performing addition is one of the simplest numerical tasks.
Addition of very small numbers is accessible to toddlers; the most basic task,
1 + 1, can be performed by infants as young as five months and even some
animals. In primary education, children learn to add numbers
in the decimal system, starting with single
digits and progressively tackling more difficult problems. Mechanical aids
range from the ancient abacus to the modern computer, where research on the most
efficient implementations of addition continues to this day.
Notation and terminology
The plus sign
Addition is written using the plus sign "+"
between the terms; that is, in infix notation. The result is expressed with an equals sign. For example,
1 + 1 = 2 (verbally,
"one plus one equals two")
2 + 2 = 4 (verbally,
"two plus two equals four")
5 + 4 + 2 = 11 (see
"associativity" below)
3 + 3 + 3 + 3 = 12 (see
"multiplication" below)
There are also situations where addition is
"understood" even though no symbol appears:
Columnar addition:
5 + 12 = 17
§ A column of numbers, with the
last number in the column underlined, usually indicates that the numbers in the column are to be
added, with the sum written below the underlined number.
§ A whole number followed
immediately by a fraction indicates
the sum of the two, called a mixed number.[2] For example,
3½ = 3 + ½ = 3.5.This notation can cause
confusion since in most other contexts juxtaposition denotes multiplication instead.
The sum of a series of
related numbers can be expressed through capital sigma notation, which compactly denotes iteration. For example,
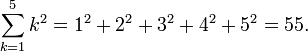
The numbers or the objects to be added in general addition
are called the "terms", the "addends", or the
"summands"; this terminology carries over to the summation of
multiple terms. This is to be distinguished from factors, which are multiplied. Some authors call the first
addend the augend. In fact, during the Renaissance, many authors did not consider
the first addend an "addend" at all. Today, due to the symmetry of
addition, "augend" is rarely used, and both
terms are generally called addends.[3]
All of this terminology derives from Latin. "Addition" and "add" are English words derived from the Latin verb addere, which is in turn a compound of ad "to" and dare "to give", from the Proto-Indo-European root *deh₃- "to give"; thus to add is to give to.[3] Using the gerundive suffix -nd results in "addend",
"thing to be added".[4] Likewise from augere "to increase", one
gets "augend", "thing to be
increased".
Redrawn illustration from The Art of Nombryng, one of the first English
arithmetic texts, in the 15th century[5]
“Sum" and "summand" derive from the Latin noun summa" the highest, the top" and associated verb summare. This is appropriate not only because the sum of two positive numbers is greater than either, but because it was once common to add upward, contrary to the modern practice of adding downward, so that a sum was literally higher than the addends.[6] Addere and summare date back at least to Boethius, if not to earlier Roman writers such as Vitruvius and Frontinus
; Boethius also used several other terms for the addition operation. The later Middle English terms "adden" and "adding" were popularized by Chaucer.[7]Interpretations
Addition is used to model countless physical processes. Even
for the simple case of adding natural numbers, there are many possible interpretations and
even more visual representations.
Combining sets
Possibly the most fundamental interpretation of addition lies
in combining sets:
§ When two or more disjoint
collections are combined into a single collection, the number of objects in the
single collection is the sum of the number of objects in the original
collections.
This interpretation is easy to visualize, with little danger
of ambiguity. It is also useful in higher mathematics; for the rigorous definition it inspires, see Natural numbers below. However, it is not
obvious how one should extend this version of addition to include fractional
numbers or negative numbers.[8]
One possible fix is to consider collections of objects that
can be easily divided, such as pies or, still better, segmented
rods.[9] Rather than just combining
collections of segments, rods can be joined end-to-end, which illustrates
another conception of addition: adding not the rods but the lengths of the
rods.
Extending a length
A second interpretation of addition comes from extending an
initial length by a given length:
§ When an original length is
extended by a given amount, the final length is the sum of the original length
and the length of the extension.
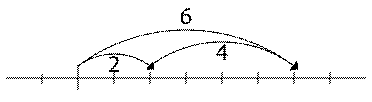
A
number-line visualization of the algebraic addition 2 + 4 = 6. A translation by 2 followed by
a translation by 4 is the same as a translation by 6.
A
number-line visualization of the unary addition 2 + 4 = 6. A translation by 4 is
equivalent to four translations by 1.
The sum a + b can be interpreted as a binary operation that combines a and b, in an algebraic
sense, or it can be interpreted as the addition of b more units to a. Under the latter
interpretation, the parts of a sum a + b play asymmetric roles, and the
operation a + b is viewed as applying the unary operation +b to a. Instead of calling both a and b addends, it is more appropriate
to call a the augend in this case, since a plays a passive role. The unary
view is also useful when discussing subtraction, because each unary addition
operation has an inverse unary subtraction operation, and vice versa.
http://www.khanacademy.org/video/basic-addition?playlist=Arithmetic
http://www.khanacademy.org/video/addition-2?playlist=Arithmetic
http://www.khanacademy.org/video/level-2-addition?playlist=Arithmetic
http://www.khanacademy.org/video/addition-3?playlist=Arithmetic
http://www.khanacademy.org/video/addition-4?playlist=Arithmetic