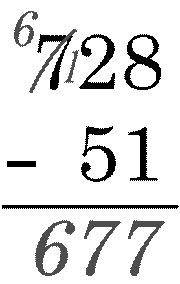Subtraction
Subtraction is one of the four basic binary arithmetic operations; it is the inverse of addition, meaning that if we start with any number and
add any number and then subtract the same number we added, we return to the
number we started with. Subtraction is denoted by a minus sign in infix notation.
An example problem
"5 − 2 =
3" (verbally, "five minus two equals three")
Since subtraction is not a commuting operator, the two operands are
named. The traditional names for the parts of the:c − b = a are minuend (c) − subtrahend (b)
= difference (a). The words
"minuend" and "subtrahend" are uncommon in modern usage.[1] Instead we say that c and−b are terms, and treat subtraction as addition of
the additive inverse. The answer is still called the difference.
Subtraction is used to model four related processes:
1.
From a
given collection, take away (subtract) a given number of objects. For example,
5 apples minus 2 apples leaves 3 apples.
2.
From a
given measurement, take away a quantity measured in the same units. If I weigh
200 pounds, and lose 10 pounds, then I weigh 200 − 10 = 190
pounds.
3.
Compare
two like quantities to find the difference between them. For example, the
difference between $800 and $600 is $800 − $600 = $200. Also
known as comparative
subtraction.
4.
To find
the distance between two locations at a fixed distance from starting point. For
example if, on a given highway, you see a mileage marker that says 150 miles
and later see a mileage marker that says 160 miles, you have traveled
160 − 150 = 10 miles.
In mathematics, it is often useful to view or even define subtraction as a kind of addition, the addition of the additive inverse. We can view 7 − 3 = 4 as the sum of two terms: 7 and -3. This perspective allows us to apply to subtraction all of the familiar rules and nomenclature of addition. Subtraction is not associative or commutative—in fact, it is anticommutative
and left-associative—but addition of signed numbers is both.Basic subtraction: integers
Imagine a line segment of length b with the left end labeled a and the right end labeled c. Starting from a, it takes b steps to the right to reach c. This movement to the right is
modeled mathematically by addition:
a + b = c.
From c, it takes b steps to the left to get back to a. This movement to the left is
modeled by subtraction:
c − b = a.
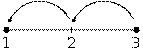
Now, imagine a line segment labeled with the numbers 1, 2, and 3. From position 3, it takes no steps to the left to stay at
3, so 3 − 0 = 3. It takes 2 steps to the left to get to
position 1, so 3 − 2 = 1. This picture is inadequate to
describe what would happen after going 3 steps to the left of position 3. To
represent such an operation, the line must be extended.
To subtract arbitrary natural numbers, one begins with a line containing every natural
number (0, 1, 2, 3, 4, 5, 6, ...). From 3, it takes 3
steps to the left to get to 0, so 3 − 3 = 0. But
3 − 4 is still invalid since it again leaves the line. The
natural numbers are not a useful context for subtraction.
The solution is to consider the integer number line (..., −3, −2, −1,
0, 1, 2, 3, ...). From 3, it takes 4 steps to the left
to get to −1:
3 − 4 = −1.
Subtraction as addition
There are some cases where subtraction as a separate operation becomes problematic. For
example, 3 − (−2) (i.e. subtract −2 from 3) is not
immediately obvious from either a natural number view or a number line view, because it is not
immediately clear what it means to move −2 steps to the right or to take
away −2 apples. One solution is to view subtraction as addition of signed
numbers. Extra minus signs simply denote additive inversion. Then we have
3 − (−2) = 3 + 2 = 5. This
also helps to keep the ring of integers "simple"
by avoiding the introduction of "new" operators such as subtraction.
Ordinarily a ring only has two operations defined on it; in the case of the
integers, these are addition and multiplication. A ring already has the concept
of additive inverses, but it does not have any notion of a separate subtraction
operation, so the use of signed addition as subtraction allows us to apply the
ring axioms to subtraction without needing to prove anything.
Algorithms for subtraction
There are various algorithms for subtraction, and they differ
in their suitability for various applications. A number of methods are adapted
to hand calculation; for example, when making
change, no actual subtraction is performed, but rather the change-maker counts
forward.
For machine calculation, the method of complements is preferred, whereby the
subtraction is replaced by an addition in a modular arithmetic.
The method by which elementary school children are taught to subtract varies from
country to country, and within a country, different methods are in fashion at
different times. In traditional mathematics, a specific process is taught
to children at the end of the 1st year or during the 2nd year for use with
multi-digit whole numbers, and is extended in either the fourth or fifth grade
to include decimal representations of fractional numbers.
American schools currently teach a method of subtraction
using borrowing and a system of markings called crutches. Although a method of
borrowing had been known and published in textbooks prior, apparently the
crutches are the invention of William A. Brownell who used them in a study in
November 1937. This system caught on rapidly, displacing the other methods of
subtraction in use in America at that time.
European children are taught, and some older Americans employ
a method of subtraction called the Austrian
method, also
known as the additions method. There is no borrowing in this method. There are
also crutches (markings to aid the memory) which vary according to country.
Both these methods break up the subtraction as a process of
one digit subtractions by place value. Starting with a least significant digit,
a subtraction of subtrahend:
sj sj−1 ... s1
from minuend
mk mk−1 ... m1,
where each si and mi is a digit, proceeds by writing
down m1 − s1, m2 − s2,
and so forth, as long as si does not exceed mi. Otherwise, mi is increased by 10 and some
other digit is modified to correct for this increase. The American method
corrects by attempting to decrease the minuend digit mi+1 by one (or continuing the borrow leftwards until there is a non-zero digit from
which to borrow). The European method corrects by increasing the subtrahend
digit si+1 by one.
Example: 704 − 512. The minuend is 704,
the subtrahend is 512. The minuend digits are m3 = 7, m2 = 0 and m1 = 4. The subtrahend digits are s3 = 5, s2 = 1 and s1 = 2. Beginning at the one's
place, 4 is not less than 2 so the difference 2 is written down in the result's
one place. In the ten's place, 0 is less than 1, so the 0 is increased to 10,
and the difference with 1, which is 9, is written down in the ten's place. The
American method corrects for the increase of ten by reducing the digit in the
minuend's hundreds place by one. That is, the 7 is struck through and replaced
by a 6. The subtraction then proceeds in the hundreds place, where 6 is not
less than 5, so the difference is written down in the result's hundred's place.
We are now done, the result is 192.
The Austrian method will not reduce the 7 to 6. Rather it
will increase the subtrahend hundred's digit by one. A small mark is made near
or below this digit (depending on the school). Then the subtraction proceeds by
asking what number when increased by 1, and 5 is added to it, makes 7. The
answer is 1, and is written down in the result's hundred's place.
There is an additional subtlety in that the child always
employs a mental subtraction table in the American method. The Austrian method
often encourages the child to mentally use the addition table in reverse. In
the example above, rather than adding 1 to 5, getting 6, and subtracting that
from 7, the child is asked to consider what number, when increased by 1, and 5
is added to it, makes 7.
http://www.khanacademy.org/video/basic-subtraction?playlist=Arithmetic
http://www.khanacademy.org/video/subtraction-2?playlist=Arithmetic
http://www.khanacademy.org/video/alternate-mental-subtraction-method?playlist=Arithmetic
http://www.khanacademy.org/video/level-4-subtraction?playlist=Arithmetic
http://www.khanacademy.org/video/why-borrowing-works?playlist=Arithmetic