Least common multiple

In arithmetic and number theory, the least common multiple (also called the lowest common multiple or smallest common multiple) of two integers a and b, usually denoted by LCM(a, b), is the smallest positive integer that is a multiple of both a and b.^[1] It is familiar from grade-school arithmetic as the "lowest common denominator" that must be determined before two fractions can be added.

This definition may be extended to rational numbers a and b: the LCM is the smallest positive rational number that is an integer multiple of both a and b. (In fact, the definition may be extended to any two real numbers whose ratio is a rational number.)

If either a or b is 0, LCM(a, b) is defined to be zero.

The LCM of more than two integers or rational numbers is well-defined: it is the smallest number that is an integer multiple of each of them.

Examples

Integer

What is the LCM of 4 and 6?

Multiples of 4 are:

4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, 64, 68, 72, 76 etc.

and the multiples of 6 are:

6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, ...

Common multiples of 4 and 6 are simply the numbers that are in both lists:

12, 24, 36, 48, 60, 72, ....

So the least common multiple of 4 and 6 is the smallest one of those: 12

Rational

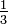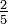What is the LCM of $\tfrac{1}{3}$ and $\tfrac{2}{5}$ ?

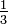The multiples of $\tfrac{1}{3}$ are:

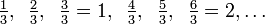
$\tfrac{1}{3},\;\;\tfrac{2}{3},\;\;\tfrac{3}{3}= 1,\;\;\tfrac{4}{3},\;\;\tfrac{5}{3},\;\;\tfrac{6}{3}=2,\dots\;\;$

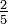and the multiples of $\tfrac{2}{5}$ are:

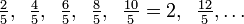
$\tfrac{2}{5},\;\;\tfrac{4}{5},\;\;\tfrac{6}{5},\;\;\tfrac{8}{5},\;\;\tfrac{10}{5}=2,\;\;\tfrac{12}{5},\dots\;\;$

Therefore, their LCM is 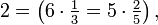$2=\left (6\cdot\tfrac{1}{3}=5\cdot\tfrac{2}{5}\right ),\;$ the smallest number on both lists.

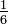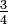What is the LCM of $\tfrac{1}{6}$ and $\tfrac{3}{4}$ ?

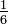The multiples of $\tfrac{1}{6}$ are:

$\tfrac{1}{6},\;\;\tfrac{2}{6}=\tfrac{1}{3},\;\;\tfrac{3}{6}=\tfrac{1}{2},\;\;\tfrac{4}{6}=\tfrac{2}{3},\;\;\tfrac{5}{6},\;\;\tfrac{6}{6}=1,\;\;\tfrac{7}{6},\;\;\tfrac{8}{6}=\tfrac{4}{3},\;\;\tfrac{9}{6}=\tfrac{3}{2},\dots,\;\;$

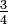and the multiples of $\tfrac{3}{4}$ are:

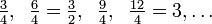
$\tfrac{3}{4},\;\;\tfrac{6}{4}=\tfrac{3}{2},\;\;\tfrac{9}{4},\;\;\tfrac{12}{4}=3,\dots\;\;$

So their LCM is 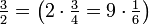$\tfrac{3}{2}=\left (2\cdot\tfrac{3}{4}=9\cdot\tfrac{1}{6}\right)$ .

Note that, by definition, if a and b are two rationals (or integers), there are integers m and n such that LCM(a, b) = m × a = n × b. This implies that m and n are coprime

; otherwise they could be divided by their common divisor, giving a common multiple less than the least common multiple, which is absurd. The above examples illustrate this fact.

When adding, subtracting, or comparing vulgar fractions, it is useful to find the least common multiple of the denominators, often called the lowest common denominator, because each of the fractions can be expressed as a fraction with this denominator. For instance,

${2\over21}+{1\over6}={4\over42}+{7\over42}={11\over42}$

where the denominator 42 was used because it is the least common multiple of 21 and 6.

Computing the least common multiple

Reduction by the greatest common divisor

The following formula reduces the problem of computing the least common multiple to the problem of computing the greatest common divisor (GCD):

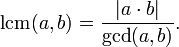
$\operatorname{lcm}(a,b)=\frac{|a\cdot b|}{\operatorname{gcd}(a,b)}.$

This formula is also valid when exactly one of a and b is 0, since gcd(a, 0) = |a|.

There are fast algorithms for computing the GCD that do not require the numbers to be factored, such as the Euclidean algorithm. To return to the example above,

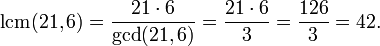
$\operatorname{lcm}(21,6) ={21\cdot6\over\operatorname{gcd}(21,6)} ={21\cdot 6\over 3}= \frac{126}{3} = 42.$

Because gcd(a, b) is a divisor of both a and b, it's more efficient to compute the LCM by dividing before multiplying:

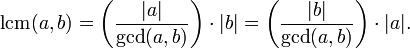
$\operatorname{lcm}(a,b)=\left({|a|\over\operatorname{gcd}(a,b)}\right)\cdot |b|=\left({|b|\over\operatorname{gcd}(a,b)}\right)\cdot |a|.$

This reduces the size of one input for both the division and the multiplication, and reduces the required storage needed for intermediate results (overflow in the a×b computation). Because gcd(a, b) is a divisor of both a and b, and thus the division will be guaranteed to yield an integer, so the intermediate result can be stored in an integer. Done this way, the previous example becomes:

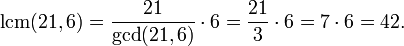
$\operatorname{lcm}(21,6)={21\over\operatorname{gcd}(21,6)}\cdot6={21\over3}\cdot6=7\cdot6=42.$

Finding least common multiples by prime factorization

The unique factorization theorem says that every positive integer greater than 1 can be written in only one way as a product of prime numbers. The prime numbers can be considered as the atomic elements which, when combined together, make up a composite number.

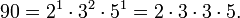
$90 = 2^1 \cdot 3^2 \cdot 5^1 = 2 \cdot 3 \cdot 3 \cdot 5. \,\!$

Here we have the composite number 90 made up of one atom of the prime number 2, two atoms of the prime number 3 and one atom of the prime number 5.

This knowledge can be used to find the lcm of a set of numbers.

Example: Find the value of lcm(8,9,21).

First, factor out each number and express it as a product of prime number powers.

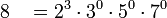
$8\; \, \; \,= 2^3 \cdot 3^0 \cdot 5^0 \cdot 7^0 \,\!$

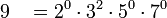
$9\; \, \; \,= 2^0 \cdot 3^2 \cdot 5^0 \cdot 7^0 \,\!$

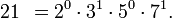
$21\; \,= 2^0 \cdot 3^1 \cdot 5^0 \cdot 7^1. \,\!$

The lcm will be the product of multiplying the highest power in each prime factor category together. Out of the 4 prime factor categories 2, 3, 5, and 7, the highest powers from each are 2³, 3², 5⁰, and 7¹. Thus,

$\operatorname{lcm}(8,9,21) = 2^3 \cdot 3^2 \cdot 5^0 \cdot 7^1 = 8 \cdot 9 \cdot 1 \cdot 7 = 504. \,\!$

This method is not as efficient as reducing to the greatest common divisor, since there is no known general efficient algorithm for integer factorization, but is useful in illustrating concepts.

This method can be illustrated using a Venn diagram as follows. Find the prime factorization of each of the two numbers. Put the prime factors into a Venn diagram with one circle for each of the two numbers, and all factors they share in common in the intersection. To find the LCM, just multiply all of the prime numbers in the diagram.

Here is an example:

48 = 2 × 2 × 2 × 2 × 3,

180 = 2 × 2 × 3 × 3 × 5,

and what they share in common is two "2"s and a "3":

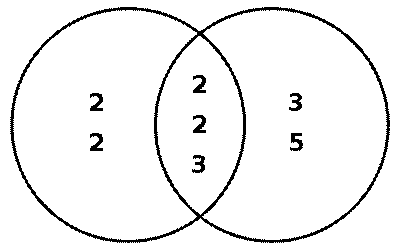
Least common multiple.svg

Least common multiple = 2 × 2 × 2 × 2 × 3 × 3 × 5 = 720

Greatest common divisor = 2 × 2 × 3 = 12

This also works for the greatest common divisor (GCD), except that instead of multiplying all of the numbers in the Venn diagram, one multiplies only the prime factors that are in the intersection. Thus the GCD of 48 and 180 is 2 × 2 × 3 = 12.

A simple algorithm

This method works as easily for finding the LCM of several integers.

Let there be a finite sequence of positive integers X = (x₁, x₂, ..., x_n), n > 1. The algorithm proceeds in steps as follows: on each step m it examines and updates the sequence X⁽^m⁾ = (x₁^(m), x₂^(m), ..., x_n^(m)), X⁽¹⁾ = X. The purpose of the examination is to pick up the least (perhaps, one of many) element of the sequence X⁽^m⁾. Assuming x_k₀⁽^m⁾ is the selected element, the sequence X^(m+1) is defined as

x_k⁽^m⁺¹⁾ = x_k⁽^m⁾, k ≠ k₀

x_k₀⁽^m⁺¹⁾ = x_k₀⁽^m⁾ + x_k₀.

In other words, the least element is increased by the corresponding x whereas the rest of the elements pass from X⁽^m⁾ to X^(m+1) unchanged.

The algorithm stops when all elements in sequence X⁽^m⁾ are equal. Their common value L is exactly LCM(X). (For a proof and an interactive simulation see reference below, Algorithm for Computing the LCM.)

A method using a table

This method works for any number of factors. One begins by listing all of the numbers vertically in a table (in this example 4, 7, 12, 21, and 42):

The process begins by dividing all of the factors by 2. If any of them divides evenly, write 2 at the top of the table and the result of division by 2 of each factor in the space to the right of each factor and below the 2. If they do not divide evenly, just rewrite the number again. If 2 does not divide evenly into any of the numbers, try 3.

http://www.khanacademy.org/video/least-common-multiple?playlist=Arithmetic