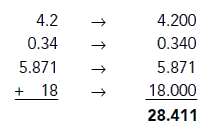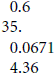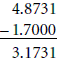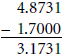Add and Subtract Decimals
Adding Decimals http://www.education.com/study-help/article/adding-subtracting-decimals/
8.17.2011
There is a crucial difference between adding decimals and
adding whole numbers; the difference is the decimal
point. The position of this point determines the
accuracy of your final answer; a problem solver cannot simply ignore the point
and add it in wherever it "looks" best. In order to add decimals
correctly, follow these three simple rules:
1.
Line the numbers up in a column so their
decimal points are aligned.
2.
Tack zeros onto the ends of shorter decimals to
keep the digits lined up evenly.
3.
Move the decimal point directly down into the
answer area and add as usual.
|
Tip The
number one pitfall in adding and subtracting decimals happens when the numbersare lined up, instead
of the decimals. Before you start
adding or subtracting with decimals, add zeros after the last digit to the
right of the decimal point to all the numbers until they each have the same
amount of digits to the right of the decimal point. For a whole number, just
add a decimal point and then add zeros to the right of it. Example:
|
Example: 3.45 +
22.1 + 0.682
|
1. |
Line
up the numbers so their decimal points are even: |
|
|
2. |
Tack
zeros onto the ends of the shorter decimals to fill in the "holes": |
|
|
3. |
Move
the decimal point directly down into the answer area and add: |
To check the reasonableness of your work, estimate the sum by using the rounding
technique you learned in Lesson 6. Round each number you added to the nearest
whole number, and then add the resulting whole numbers. If the sum is close to
your answer, your answer is in the ballpark. Otherwise, you may have made a mistake
in placing the decimal point or in the adding. Rounding 3.45, 22.1, and 0.682
gives you 3, 22, and 1. Their sum is 26, which is reasonably close to your actual answer of 26.232. Therefore, 26.232 is a reasonable answer.
Look at an example that adds decimals and whole numbers
together. Remember: A whole number is understood to have a decimal point to its
right.
Example: 0.6 + 35 + 0.0671 + 4.36
|
1. |
Put
a decimal point at the right of the whole number (35) and line up the numbers
so their decimal points are aligned: |
|
|
2. |
Tack
zeros onto the ends of the shorter decimals to fill in the "holes": |
|
|
3. |
Move
the decimal point directly down into the answer area and add: |
Subtracting Decimals
When subtracting decimals, follow the same initial steps as
in adding to ensure that you're adding the correct digits and that the decimal
point ends up in the right place.
Example: 4.8731 – 1.7
|
1. |
Line
up the numbers so their decimal points are aligned: |
|
|
2. |
Tack
zeros onto the end of the shorter decimal to fill in the "holes": |
|
|
3. |
Move
the decimal point directly down into the answer and subtract: |
Subtraction is easily checked by adding the number that was
subtracted to the difference (the answer). If you get back the other number in
the subtraction problem, then your answer is correct. For example, let's check
our last subtraction problem.
|
|
Here's
the subtraction: |
|
|
1. |
Add
the number that was subtracted (1.7000) to the difference (3.1731): |
|
|
2. |
The
subtraction is correct because we got back the other number in the
subtraction problem (4.8731). |
Checking your subtraction is so easy that you should never
pass up the opportunity!
You can check the reasonableness of your work by estimating: Round each number to the nearest
whole number and subtract. Rounding 4.873 and 1.7 gives 5 and
2. Since their difference of 3 is close to your actual answer, 3.1731 is reasonable.
|
Tip When
subtracting mixed decimals gets rid of any whole numbers, write a zero in the
ones place. Example: 5.67 – 4.9 = 0.77, and should not
be written as .77. |