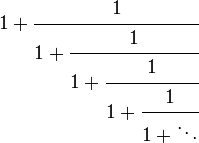Golden ratio

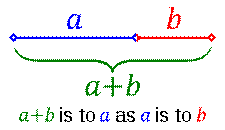
http://upload.wikimedia.org/wikipedia/commons/thumb/4/44/Golden_ratio_line.svg/225px-Golden_ratio_line.svg.png

http://bits.wikimedia.org/skins-1.17/common/images/magnify-clip.png

The golden section is a line segment divided according to the golden ratio: The total length a + b is to the length of the longer segment a as the length of a is to the length of the shorter segment b.

In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989.[1] Other names frequently used for the golden ratio are the golden section (Latin: sectio aurea) and golden mean.[2][3][4] Other terms encountered include extreme and mean ratio,[5] medial section, divine proportion, divine section(Latin: sectio divina), golden proportion, golden cut,[6] golden number, and mean of Phidias.[7][8][9] In this article the golden ratio is denoted by the Greek lowercase letter phi (\varphi \,), while its reciprocal, 1/\varphi \, or \varphi^{-1} \,, is denoted by the uppercase variant Phi (\Phi\,).

The figure on the right illustrates the geometric relationship that defines this constant. Expressed algebraically:

\frac{a+b}{a} = \frac{a}{b} \equiv \varphi\,.

This equation has one positive solution in the set of algebraic irrational numbers:

\varphi = \frac{1+\sqrt{5}}{2} = 1.61803\,39887\ldots.\, [1]

At least since the Renaissance, many artists and architects have proportioned their works to approximate the golden ratio—especially in the form of the golden rectangle, in which the ratio of the longer side to the shorter is the golden ratio—believing this proportion to be aesthetically pleasing (see Applications and observations below). Mathematicians have studied the golden ratio because of its unique and interesting properties. The golden ratio is also used in the analysis of financial markets, in strategies such as Fibonacci retracement.

http://upload.wikimedia.org/wikipedia/commons/thumb/3/32/Golden_Rectangle_Construction.svg/220px-Golden_Rectangle_Construction.svg.png

http://bits.wikimedia.org/skins-1.17/common/images/magnify-clip.png

Construction of a golden rectangle:
1. Construct a unit square (red).
2. Draw a line from the midpoint of one side to an opposite corner.
3. Use that line as the radius to draw an arc that defines the long dimension of the rectangle.

http://upload.wikimedia.org/wikipedia/commons/thumb/8/8e/SimilarGoldenRectangles.svg/220px-SimilarGoldenRectangles.svg.png

http://bits.wikimedia.org/skins-1.17/common/images/magnify-clip.png

A golden rectangle with longer side aand shorter side b, when placed adjacent to a square with sides of length a, will produce a similar golden rectangle with longer side a + b and shorter side a. This illustrates the relationship  \frac{a+b}{a} = \frac{a}{b} \equiv \varphi\,.

 

 

 

Calculation

List of numbers – Irrational and suspected irrational numbers
γ – ζ(3) – √2 – √3 – √5 – φ – ρ – δS

 – α – e – π – δ

Binary

1.1001111000110111011…

Decimal

1.6180339887498948482…

Hexadecimal

1.9E3779B97F4A7C15F39…

Continued fraction

1 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{1 + \ddots}}}}

Algebraic form

\frac{1 + \sqrt{5}}{2}

Infinite series

\frac{13}{8}+\sum_{n=0}^{\infty}\frac{(-1)^{(n+1)}(2n+1)!}{(n+2)!n!4^{(2n+3)}}

Two quantities a and b are said to be in the golden ratio φ if:

\frac{a+b}{a} = \frac{a}{b} = \varphi\,.

One method to find the value of φ is to start with the left fraction. Through simplifying the fraction and substituting in b/a = 1/φ,

\frac{a+b}{a} = 1 + \frac{b}{a} = 1 + \frac{1}{\varphi},

it is shown that,

1 + \frac{1}{\varphi} = \varphi.

Multiplying by φ gives

\varphi + 1 = \varphi^2,

which can be rearranged to

{\varphi}^2 - \varphi - 1 = 0.

Using the quadratic formula gives the only positive solution as,

\varphi = \frac{1 + \sqrt{5}}{2} = 1.61803\,39887\dots.\,