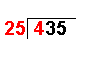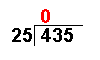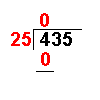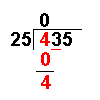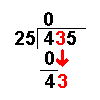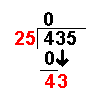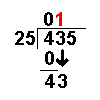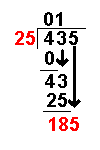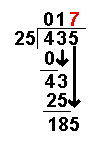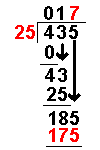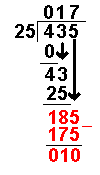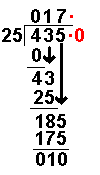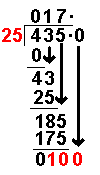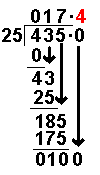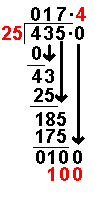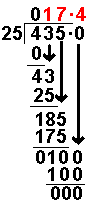Long Division to Decimal Places
http://www.mathsisfun.com/long_division3.html 8.17.2011

When we are given a long division to do it will not always work out to a whole number. Sometimes there will be numbers left over. We can use the long division process to work out the answer to a number of decimal places.

The secret to working out a long division to decimal places is the ability to add zeros after the decimal point.

Example: 150 is the same as 150.00

We can add as many zeros as we wish after the decimal point without altering the numbers value.

We will use the example below. It works out neatly to one decimal place

435 ÷ 25

	4 ÷ 25 = 0 remainder 4	The first number of the dividend is divided by the divisor.
		The whole number result is placed at the top. Any remainders are ignored at this point.
	25 × 0 = 0	The answer from the first operation is multiplied by the divisor. The result is placed under the number divided into.
	4 – 0 = 4	Now we take away the bottom number from the top number.
		Bring down the next number of the dividend.
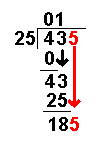
	43 ÷ 25 = 1 remainder 18	Divide this number by the divisor.
		The whole number result is placed at the top. Any remainders are ignored at this point.
	25 × 1 = 25	The answer from the above operation is multiplied by the divisor. The result is placed under the last number divided into.
	43 – 25 = 18	Now we take away the bottom number from the top number.
		Bring down the next number of the dividend.
	185 ÷ 25 = 7 remainder 10	Divide this number by the divisor.
		The whole number result is placed at the top. Any remainders are ignored at this point.
	25 × 7 = 175	The answer from the above operation is multiplied by the divisor. The result is placed under the number divided into.
	185 – 175 = 10	Now we take away the bottom number from the top number.
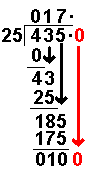
		Now we have reached the end of the whole numbers we add a decimal place and the first zero. Notice the decimal point which has appeared on the answer line and by the dividend. It does not appear anywhere else.
		Bring down the next number of the dividend.
	100 ÷ 25 = 4 remainder 0	Divide this number by the divisor.
		The whole number result is placed at the top. Any remainders are ignored at this point.
	25 × 4 = 100	The answer from the above operation is multiplied by the divisor. The result is placed under the number divided into.
	100 – 100 = 0	Now we take away the bottom number from the top number.
		The subtraction has given zero. We stop when this happens. The answer will be 17.4  As long as the subtraction gives a number above zero the long division can carry on to as many decimal places as we wish. Answer: 435 ÷ 25 = 17.4