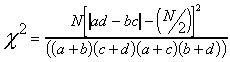
Chi square
NOMINAL DATA: Inference
A. Chi square (for 2 x 2 tables):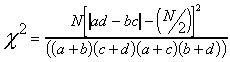
Assumptions:
1) independent variables
2) every fe > 5
3) requires a large sample of 100 or more if not normally distributed
also: d.f. = (R - 1)(C - 1)
where: R = number of rows & C = number of columns
Example:
| MALE | FEMALE | ||
| YES | 63 | ||
| NO | 37 | ||
| 100 |
Does sexually explicit materials lead to rape?
Q: Can this association be generalized to the whole population?
A: 100(|22(18) - 19(41)|- 100/2 )2 = 11,088,900
= 1.967
----(63)(37)(41)(59) -----------------5,638,689
Interpretation: Use table (see appendix).
Portion of a Chi square table:
d.f. p =.05 p = .01
1 ------3.84 ----6.64
2 ------5.99 ----9.21
3------ : --------:
Compute degrees of freedom
Example (above): d.f.= (R - 1)(C - 1)
= (2 - 1)(2 - 1)
= 1(1) = 1
Look on table: with d.f. = 1, if 2 = 3.84, p = .05.
If 2 = 6.64, p = .01. The example 2 = 1.97
Imagine that the table is a continuum:
p > .05 p = .05 p < .05 p = .01 p < .01
0 -1.97----3.84-------------- 6.64
can't can generalize
So the answer to the question: No, one cannot generalize because
p >.05 (which means that the chances of being wrong is greater
than 5/100).
Size of the sample affects the outcome, greater the size, greater
the inferential power of the analysis. If the sample had been
quadrupled in size, what would have been the outcome?
Example: 400(|88(72) - 76(164)| - 400/2)2
= 9.74
--------------(164)(236)(148)(252)
Now, the chances of being wrong is less than 1/100. One can generalize
to the whole population.
B. Chi square for any size table: 
= [(fo
- fe)2] / fe
Where: fo = number in a cell
fe = (row total)(column total)
------------------N
Assumptions: 1) independent variable 2) every fe > 5
Also: d.f. = (R - 1)(C - 1)
Example:
| 438 | |||
| 200 | |||
| 218 | |||
| 856 |
Q: Is this sample association inferable to the whole population?
A: Make a table to compute data:
| fo | fe | fe | fo - fe | (fo - fe)2 | [(fo - fe)2] / fe |
| 193 | [(438)(407)]/856 | 208.3 | -15.3 | 234.1 | 1.12 |
| 92 | [(200)(407)]/856 | 95.1 | -3.1 | 9.6 | .10 |
| 122 | [(218)(407)]/856 | 103.7 | 18.3 | 334.9 | 3.23 |
| 245 | [(438)(449)]/856 | 229.7 | 15.3 | 234.1 | 1.02 |
| 108 | [(200)(449)]/856 | 104.9 | 3.1 | 9.6 | .09 |
| 96 | [(218)(449)]/856 | 114.3 | -18.3 | 334.9 | 2.93 |
| 856* | 0* | 8.49 |
*These totals must = N and 0, respectively, or a math error was made!.
= 8.49; but it can't be used as it is.
Must know degrees of freedom: d.f. = (3 - 1)(2 - 1) = 2
Look at chart: For 2 d.f., p = .05 = 5.99, p=.01 = 9.21; the answer
is between these values. p =.05 = 5.99
= 8.49 p = .01 = 9.21
So the answer to question is: Yes, one can expect to find this relationship in a larger population (since p value is < .05)