TABULAR PRESENTATION OF DATA

Raw Data

Ungrouped Data	Grouped Data
Ages	Ages	f or	Ages	f
25	18	2	18-19	5
45	19	3	20-21	23
22	20	11	22-23	22
23	21	12	24-25	6
46	22	15	26-27	4
84	23	7	28-29	etc.
12	24	4	30-31
2	25	2	32-33
34	26	3	34-35
15	27	1	etc.

* note the difference is width of category; 1 versus 2 years

1. How to group data: some guidelines
   
   • Number of categories should be great enough so accuracy is not sacrificed too much.
     Example of too much:
     

Ages	f
18-31	72
32-45	45

• Number of categories should be small enough to avoid vacant categories or great fluctuations between categories.
  
• All categories should be equal in width (this is especially important).

1. 2. Almost every measurement is rounded off, such as height ("5 foot 9 inches" instead of "5 foot 8.89 inches"). One major exception to this is age. Age is looked at two ways:
   

	Age to last Birthday					Age to nearest Birthday
Age limits		True limits	midpoint		Age limits		true limits	midpoint
18-19		18.00-19.999	19.00		18-19		17.50-19.4999	18.5
20-21		20.00-21.999	21.00		20-21		19.50-21.4999	20.5 etc.

m (for continuous variables) =

m (for discrete variables) =

*midpoint: abbreviated : "m"

*discrete variable: the variable's unit of measure cannot be divided infinitely

*continuous variable: the variable's unit of measure that can be divided infinitely.

GRAPHING DATA

1. Histogram -- for interval data
   • width of rectangle = width of category
   • rectangles are centered over the midpoints of the category
   • rectangles are connected to each other to indicate their continuous nature

B. Bar graph -- for nominal data (or ordinal)

• order is irrelevant unless using ordinal data
• bars can be of any width, but are all equal in width

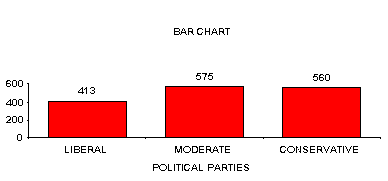
^{SOURCE: GSS91 SURVEY SUBSAMPLE}

C. Pie Chart -- for nominal data (or ordinal)

• slices are proportional in width
• order is irrelevant unless using ordinal data

^{SOURCE: GSS91 SURVEY SUBSAMPLE}

*Double hatch marks indicate interruption in the consistently equal intervals. In this case the earliest age in the sample was 15. The double hatch marks indicates that the range 0-9.99 was skipped in the polygon.

D. Frequency polygon -- for interval data

• often used for scientific purposes
• need midpoints; plot these
• connect the dots
  

TYPES OF DISTRIBUTION

A. unimodal = one peak (mode)

• "normal curve," "Bell shape distribution"
• symmetrical (right side = left)

B. bimodal = 2 modes

C. Skewed distributions are unimodal distributions which are not symmetrical. A positively skewed distribution will have a mean that is greater in value than its median. Its tail will fall on the side of the larger values. A negatively skewed distribution will have a median that is greater in value than it's mean. Its tail will fall on the side of the smaller values. A normal curve skew measures 0, while a positive skew measure is a positive value and the negative skew measure is a negative value.

D. Degree of kurtosis -- more dense or peaked distributions than the Bell curve are called leptokurtic. Flatter distributions than the Bell curve are called platykurtic. A normal kurtosis measures 0. A positive value of kurtosis describes a leptokurtic distribution, while a negative value of kurtosis describes a platykurtic distribution.

table of contents

next lesson